Filtered category
In category theory, filtered categories generalize the notion of directed set understood as a category (hence called a directed category; while some use directed category as a synonym for a filtered category).
A category  is filtered when
is filtered when
- it is not empty,
- for every two objects
 and
and 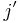 in
in  there exists an object
there exists an object  and two arrows
and two arrows 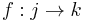 and
and 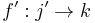 in
in  ,
, - for every two parallel arrows
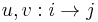 in
in  , there exists an object
, there exists an object  and an arrow
and an arrow 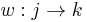 such that
such that 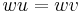 .
.
A diagram is said to be of cardinality  if the morphism set of its domain is of cardinality
if the morphism set of its domain is of cardinality  . A category
. A category  is filtered if and only if there is a cone over any finite diagram
is filtered if and only if there is a cone over any finite diagram 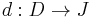 ; more generally, for a regular cardinal
; more generally, for a regular cardinal  , a category
, a category  is said to be
is said to be  -filtered if for every diagram
-filtered if for every diagram  in
in  of cardinality smaller than
of cardinality smaller than  there is a cone over
there is a cone over  .
.
A filtered colimit is a colimit of a functor 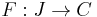 where
where  is a filtered category. This readily generalizes to
is a filtered category. This readily generalizes to  -filtered limits. An ind-object in a category
-filtered limits. An ind-object in a category  is a presheaf of sets
is a presheaf of sets 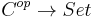 which is a small filtered colimit of representable presheaves. Ind-objects in a category
which is a small filtered colimit of representable presheaves. Ind-objects in a category  form a full subcategory
form a full subcategory 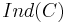 in the category of functors
in the category of functors 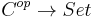 . The category
. The category 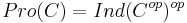 of pro-objects in
of pro-objects in  is the opposite of the category of ind-objects in the opposite category
is the opposite of the category of ind-objects in the opposite category 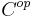 .
.
Cofiltered categories
There is a dual notion of cofiltered category. A category  is cofiltered if the opposite category
is cofiltered if the opposite category 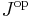 is filtered. In detail, a category is cofiltered when
is filtered. In detail, a category is cofiltered when
- it is not empty
- for every two objects
 and
and 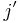 in
in  there exists an object
there exists an object  and two arrows
and two arrows 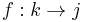 and
and 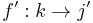 in
in  ,
, - for every two parallel arrows
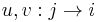 in
in  , there exists an object
, there exists an object  and an arrow
and an arrow 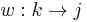 such that
such that 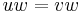 .
.
A cofiltered limit is a limit of a functor 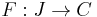 where
where  is a cofiltered category.
is a cofiltered category.
References
- Artin, M. , Grothendieck, A. and Verdier, J. L. Séminaire de Géométrie Algébrique du Bois Marie (SGA 4). Lecture Notes in Mathematics 269, Springer Verlag, 1972. Exposé I, 2.7.
- Mac Lane, Saunders (1998), Categories for the Working Mathematician (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-98403-2, section IX.1.